动态规划-基础题
斐波那契数-509
题目描述
斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。
示例 1：
输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2：
输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3：
输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3
解题思路
$F(n)$表示第n个斐波那契数，则有状态转移方程：
\[F(n) = \begin{cases} 0, & \text{if } n = 0 \\[6pt] 1, & \text{if } n = 1 \\[6pt] F(n-1) + F(n-2), & \text{if } n > 1 \end{cases}\]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func fib(n int) int {
if n == 0 {
return 0
}
dp := make([]int, n+1)
dp[0] = 0
dp[1] = 1
for i := 2; i < n+1; i++ {
dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}
爬楼梯-70
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
示例 1：
输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2：
输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
提示：
1 <= n <= 45
解题思路
设$S(n)$表示爬到第n阶楼梯的方法数，n-1处，可以再爬1阶可以登顶, 有$S(n-1)$种方方式； n-2处，可以再爬2阶也可以登顶，有$S(n-2)$种方式。因此也是斐波那契问题，状态转移方程为：
\[S(n) = \begin{cases} 1, & \text{if } n = 1 \\[6pt] 2, & \text{if } n = 2 \\[6pt] S(n-1) + S(n-2), & \text{if } n > 2 \end{cases}\]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func climbStairs(n int) int {
if n == 1 {
return 1
}
dp := make([]int, n+1)
dp[1] = 1
dp[2] = 2
for i := 3; i < n+1; i++ {
dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}
使用最小花费爬楼梯-746
题目描述
给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
示例 1：
输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。
- 支付 15 ，向上爬两个台阶，到达楼梯顶部。
总花费为 15 。
示例 2：
输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。
- 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
- 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
- 支付 1 ，向上爬一个台阶，到达楼梯顶部。
总花费为 6 。
提示：
2 <= cost.length <= 1000
0 <= cost[i] <= 999
解题思路
设$S(n)$表示到达第n阶楼梯的最小花费，则可以在n-1阶楼梯处，支付cost[n-1]，再爬1阶到达n阶； 也可以在n-2阶楼梯处，支付cost[n-2]，再爬2阶到达n阶。取两者的最小值。 因此状态转移方程为：
关键点：
可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯；意味着下标为 0 或下标为 1 的台阶花费为 0。
下标为 len(cost) 是楼顶，而不是 len(cost)-1。所以登顶最低费用为 dp[len(cost)]。
cost 1 100 1 1 1 100 1 1 100 1 楼顶 下标 0 1 2 3 4 5 6 7 8 9 10 dp数组 0 0 1 2 2 3 3 4 4 5 6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
func minCostClimbingStairs(cost []int) int {
dp := make([]int, len(cost)+1) // 第i个台阶的最小花费，i从0开始；下标 len(cost) 代表楼顶
// 可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯，意味着初始花费为 0
dp[0] = 0
dp[1] = 0
for i := 2; i < len(cost)+1; i++ {
dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])
}
// 下标 len(cost) 代表到达楼顶
return dp[len(cost)]
}
不同路径-62
题目描述
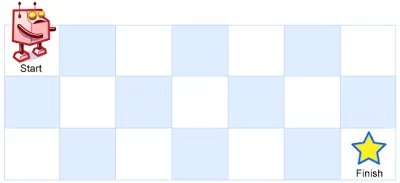
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。 问总共有多少条不同的路径？
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
示例 1：
输入：m = 3, n = 7
输出：28
示例 2：
输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3：
输入：m = 7, n = 3
输出：28
示例 4：
输入：m = 3, n = 3
输出：6
提示：
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9
解题思路
设$S(m,n)$表示单元格（m, n）的不同路径数，则等于正上方单元格（m-1, n）的不同路径数向下走一步， 加上左方单元格（m, n-1）的不同路径数向右走一步。因此状态转移方程为：
\[S(m,n) = \begin{cases} 1, & \text{if } m = 1 \text{ or } n = 1 \\[6pt] S(m-1,n) + S(m,n-1), & \text{if } m > 1 \text{ and } n > 1 \end{cases}\]关键点：
- 边界条件：第 1 行和第 1 列的单元格只有 1 条路径。
- 到某个单元格的路径数，依赖左方和正上方单元格
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func uniquePaths(m int, n int) int {
// 边界条件: m = 1或者 n = 1时，只有一条路径
table := make([][]int, m)
for r := 0; r < m; r++ { // 构建初始表格，第一行和第一列初始化为1
row := make([]int, n)
if r == 0 {
for c := 0; c < n; c++ {
row[c] = 1
}
table[r] = row
continue
}
row[0] = 1
table[r] = row
}
for r := 1; r < m; r++ {
for c := 1; c < n; c++ {
// 动态规划转移方程
table[r][c] = table[r][c-1] + table[r-1][c]
}
}
return table[m-1][n-1]
}
不同路径 II-63
题目描述
给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角（即 grid[0][0]）。机器人尝试移动到 右下角（即 grid[m - 1][n - 1]）。机器人每次只能向下或者向右移动一步。
网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。
返回机器人能够到达右下角的不同路径数量。
测试用例保证答案小于等于 2 * 109。
示例 1：
输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] 输出：2 解释：3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有 2 条不同的路径：
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右
示例 2：
输入：obstacleGrid = [[0,1],[0,0]] 输出：1
提示：
- m == obstacleGrid.length
- n == obstacleGrid[i].length
- 1 <= m, n <= 100
- obstacleGrid[i][j] 为 0 或 1
解题思路
设$S(i,j)$表示单元格（i, j）的不同路径数，则等于正上方单元格（i-1, j）的不同路径数向下走一步， 加上左方单元格（i, j-1）的不同路径数向右走一步。
当单元格（i, j）存在障碍物，$S(m,n)$等于 0，此路不通。
因此状态转移方程为：
\[S(i,j) = \begin{cases} 0, & \text{if } obstacleGrid[i][j] = 1 \\[6pt] 1, & \text{if } m = 1 \text{ and } n = 1 \\[6pt] S(i,j-1), & \text{if } i = 0 \text{ and } j > 0 \\[6pt] S(i-1,j), & \text{if } i > 0 \text{ and } j = 0 \\[6pt] S(i,j-1) + S(i-1,j), & \text{if } i > 0 \text{ and } j > 0 \end{cases}\]
注意点：
- 当obstacleGrid[i][j] == 1表示有障碍物，此路不通，则$S(i,j) = 0$
- 临界条件：出发点有障碍物；第一行（i=0）,第一列（j=0）;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func uniquePathsWithObstacles(obstacleGrid [][]int) int {
for r := 0; r < len(obstacleGrid); r++ {
for c := 0; c < len(obstacleGrid[0]); c++ {
if obstacleGrid[r][c] == 1 { // 有障碍物；此路不通
obstacleGrid[r][c] = 0
continue
}
if r == 0 && c == 0 { // 出发点，且没有障碍物
obstacleGrid[r][c] = 1
continue
}
if r == 0 { // 第一行；正上方无数据，只依赖左方
obstacleGrid[r][c] = obstacleGrid[r][c-1]
continue
}
if c == 0 { // 第一列；左方没数据，只依赖上方
obstacleGrid[r][c] = obstacleGrid[r-1][c]
continue
}
// 排除以上场景，当前单元格所有不同路径
// 1 、左方单元格，右移一步
// 2 、上方单元格，下移一步
obstacleGrid[r][c] = obstacleGrid[r][c-1] + obstacleGrid[r-1][c]
}
}
return obstacleGrid[len(obstacleGrid)-1][len(obstacleGrid[0])-1]
}
整数拆分-343
题目描述
给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示:
2 <= n <= 58
解题思路
S(i)表示数字 i 拆分最大乘积，将数字 i 拆分成 j 和 i-j，S(i) = S(j) * S(i-j)。
但是我们并不知道从哪里拆分 i 乘积最大，只能从 1 开始尝试。 i 拆分成 [1, i-1]和[i-1, 1]结果一致，所以只需要到i/2结束，取最大值：
1
2
3
4
5
6
7
8
9
10
for i {
maxResult := 0
for j := 1; j <= i/2; j ++ {
if dp[j] * dp[i-j] > maxResult {
maxResult = dp[j] * dp[i-j]
}
}
dp[i] = maxResult
}
j存在个别情况：j=3，此时拆分最大乘积 dp[3] = 2，不拆分最大值是 3，所以需要 max 比较一下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
for i {
maxResult := 0
for j := 1; j <= i/2; j ++ {
if dp[j] * dp[i-j] > maxResult {
left := max(dp[j], j)
right := max(dp[i-j], i-j)
if left * right > maxResult{
maxResult = left * right
}
}
}
dp[i] = maxResult
}
主体已经完成，剩下就是边界条件：dp[1] = 1, i从 2 开始遍历，自底向上填充 dp 数组。
| dp | 0 | 1 | 1 | 2 | 4 | 6 | 9 | 12 | 18 | 27 | 36 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
综上，转移方程：
\[S(i) = \begin{cases} 0 & \text{if } i = 1 \\[6pt] 1 & \text{if } i = 1 \\[6pt] S(j) * S(i-j) & \text{if } i > 1 \text{and } j > 0 \text{ and } j <= i/2 \\[6pt] \end{cases}\]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func integerBreak(n int) int {
if n <= 1 {
return 1
}
// d[i] 表示拆分数字 i 得到最大乘积
// 下标和数字 i 同步，不用做-1 操作
dp := make([]int, n+1)
//dp[0] = 0 // 没有用到 dp[0]
dp[1] = 1 // 初始条件
// 最底向上，求 dp[i]
for i := 2; i < n+1; i++ {
maxResult := 0
// 第一步把 i 拆分成 2 个数字，但是不知道从哪里拆，所以从 j=1 开始尝试
// 转移方程：dp[i] = max(dp[j] * dp[i-j])
// 另外需要注意：个别场景下，数字不拆分值更大，如：3 拆分最大乘积是 2，比自身小
for j := 1; j <= i/2; j++ {
left := max(dp[j], j) // 和自身对比，不拆分可能值更大，如：j=3
right := max(dp[i-j], i-j) // 和自身对比，不拆分可能值更大，如：j=3
if left*right > maxResult {
maxResult = left * right
}
}
dp[i] = maxResult
}
return dp[n]
}
不同的二叉搜索树-96
题目描述
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。
示例 1： 
输入：n = 3 输出：5
示例 2：
输入：n = 1 输出：1
提示： 1 <= n <= 19
解题思路
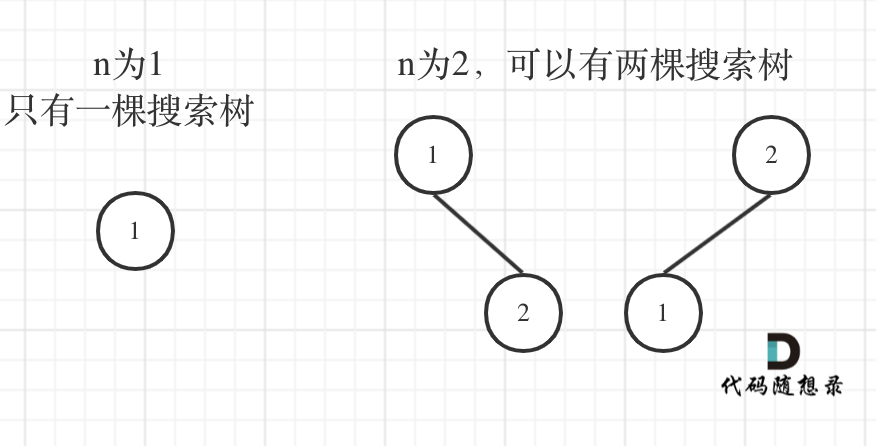
二叉搜索树：任意一个节点，其左节点都小于该节点，右节点都大于该节点，“左小右大”的排序规则二叉树
n 等于 1和2，不同搜索树： 
n 等于 3，不同搜索树： 
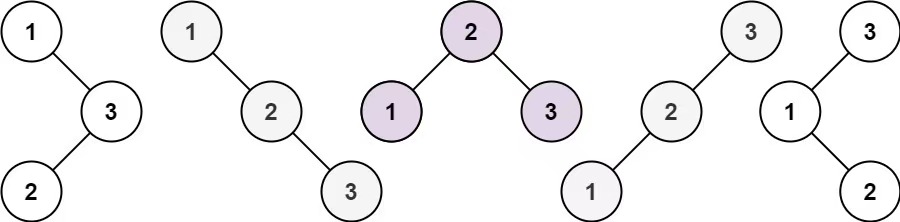
- 根节点为 1：左边有 0 个节点；右边有 2 个节点，布局与 n=2 一致（忽略数值）。
- 根节点为 2：左右两边各一个节点，布局与 n=1 一致。
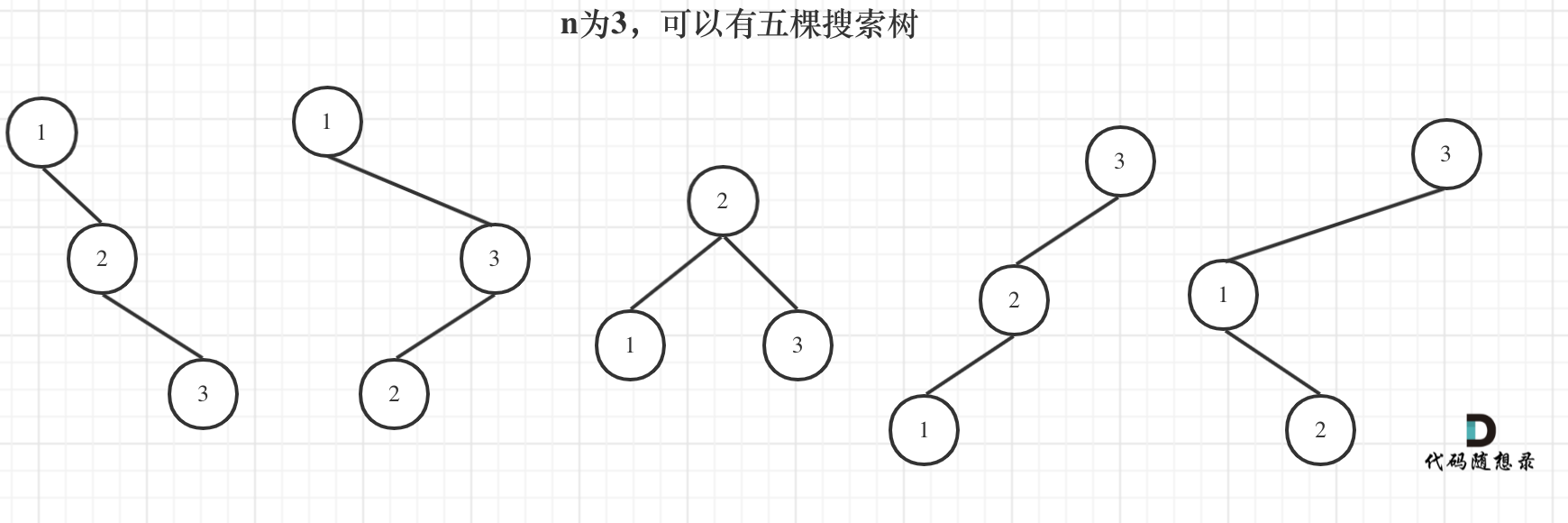
- 根节点为 3：左边有 2 个节点，布局与 n=2 一致；右边有 0 个节点。
设 dp[i] 表示i节点的不同搜索树。 所以 n=3 的所有不同搜索树：dp[3] = dp[0] * dp[2] + dp[1] * dp[1] + dp[2] * dp[0]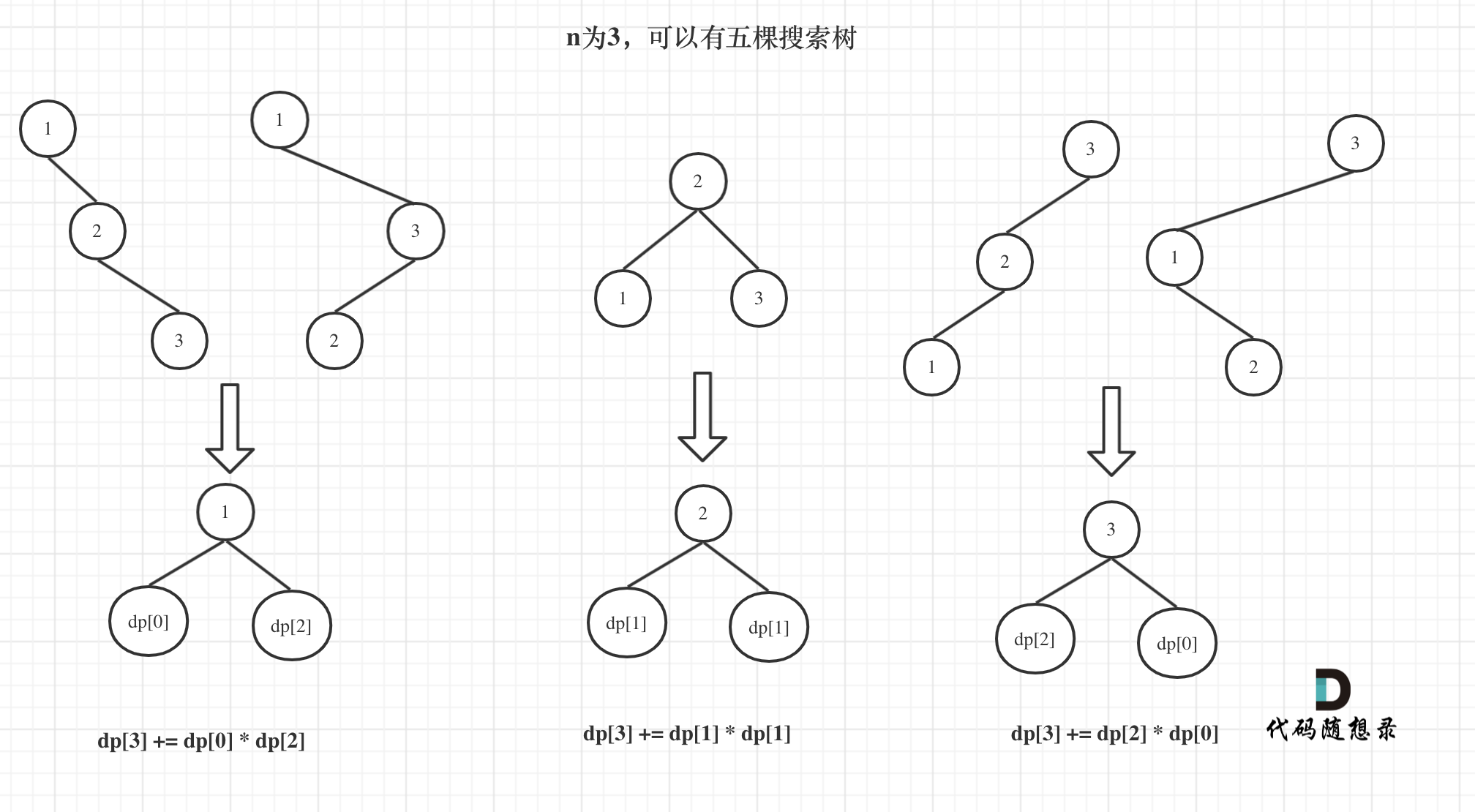 
状态转移方程：
\[dp(i) = \begin{cases} 1 & \text{if } i = 0 \\[6pt] dp(i) + dp(j-1) * dp(i-j) & \text{if } j > 0 \text{ and } j <= i \\[6pt] \end{cases}\]1
2
3
4
5
6
7
8
9
10
11
12
func numTrees(n int) int {
dp := make([]int, n+1)
dp[0] = 1
for i := 1; i < n+1; i++ {
for j := 1; j <= i; j++ {
dp[i] = dp[i] + dp[j-1]*dp[i-j]
}
}
return dp[n]
}
参考：https://github.com/youngyangyang04/leetcode-master/blob/master/problems/0096.%E4%B8%8D%E5%90%8C%E7%9A%84%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91.md