背包问题
0-1背包问题
题目描述
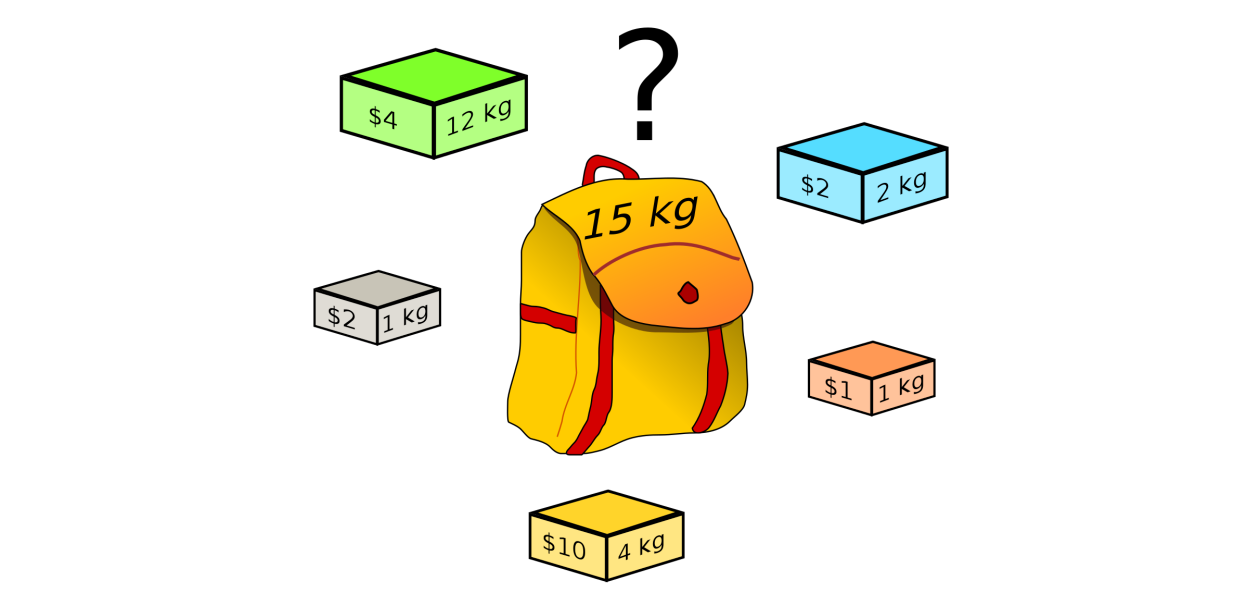
一共有N件物品,第i(i从1开始)件物品的体积为w[i],价值为v[i]。在总体积不超过背包上限C的情况下,能够装入背包的最大价值是多少?
如:
1
2
3
4
5
6
物品1: weight=7, value=42
物品2: weight=3, value=12
物品3: weight=4, value=40
物品4: weight=5, value=25
背包容量C=10; 则最大价值为: 40 + 25 = 65
解题思路
$S(i, c)$ 表示对与第 i 件物品,容量为 c 的背包,能获取的最大价值。则对于第 i 件物品,有放入和不放入两种选择:
1、不放入: 第 i 件物品重量超过背包容量,$w_i > c$。则只能选择不放入,$S(i, c) = S(i-1, c)$。
2、放入: 第 i 件物品重量不超过背包容量,$w_i \le c$。则可以选择放入,$S(i, c) = S(i-1, c - w_i) + v_i$。 $v_i$可能是负数,所以需要和不放入情况对比,取最大值。则$S(i, c) = max(S(i-1, c), s(i, c - w_i) + v_i)$
3、临界条件: 当没有物品或者背包容量为0时,最大价值为0,即$S(0, c) = 0$或$S(i, 0) = 0$。
综上所述,状态转移方程如下:
动态规划-自底向上
从解决子问题出发,逐步解决大问题。
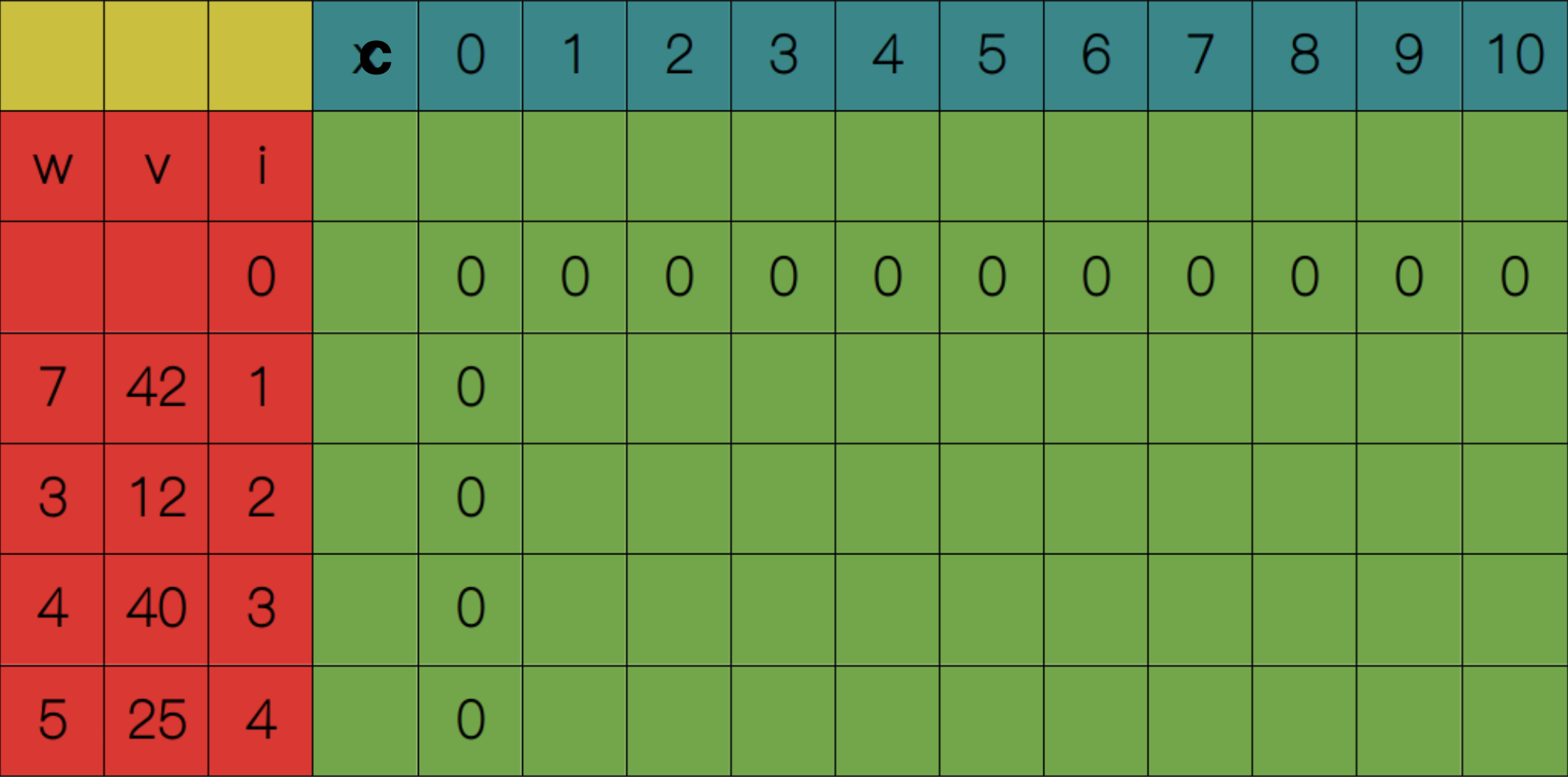
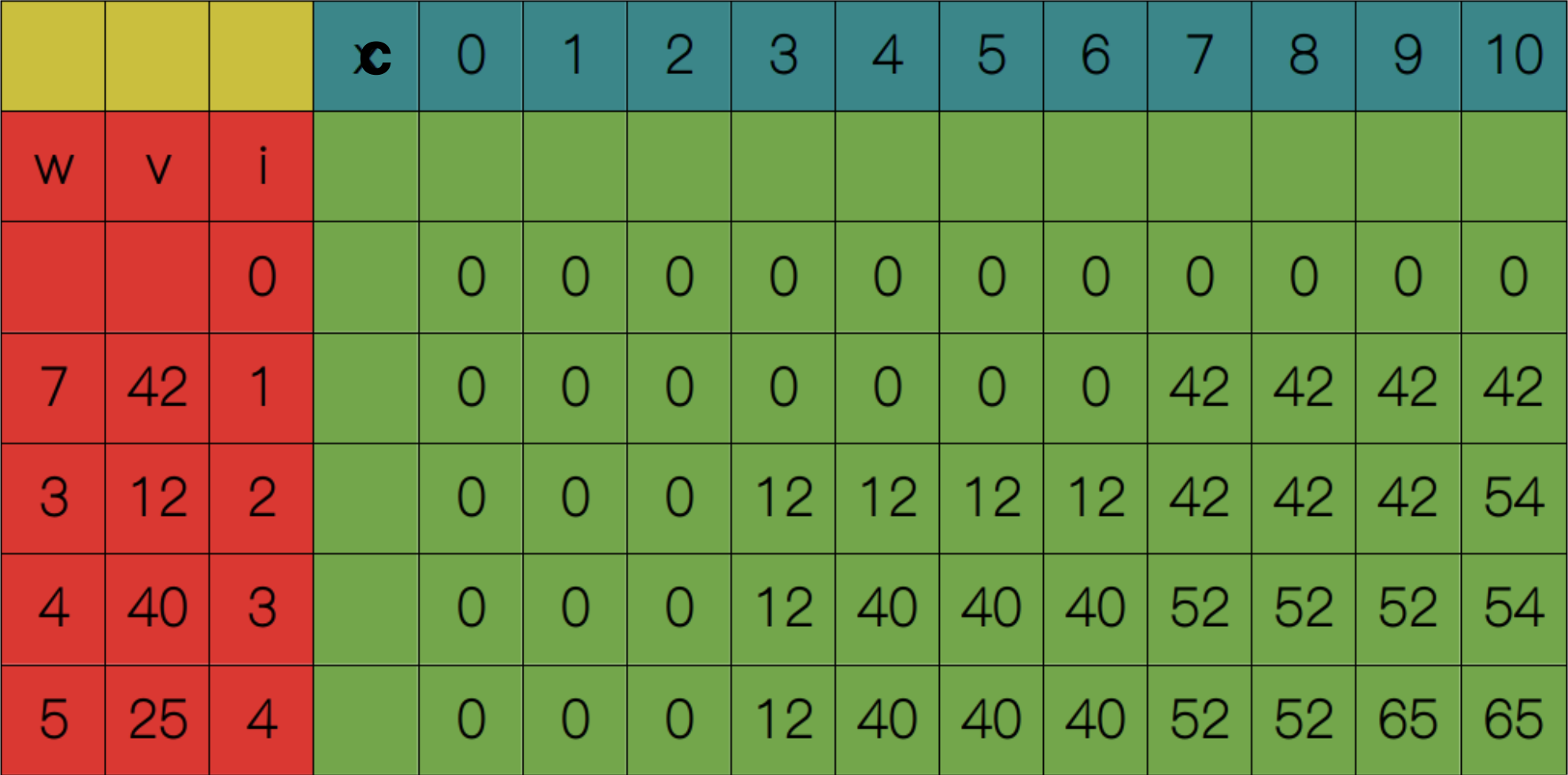
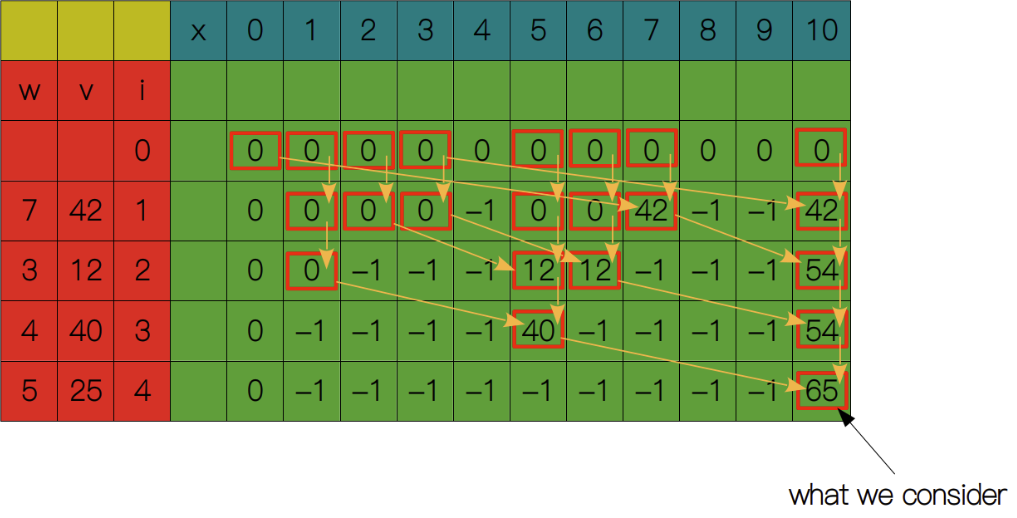
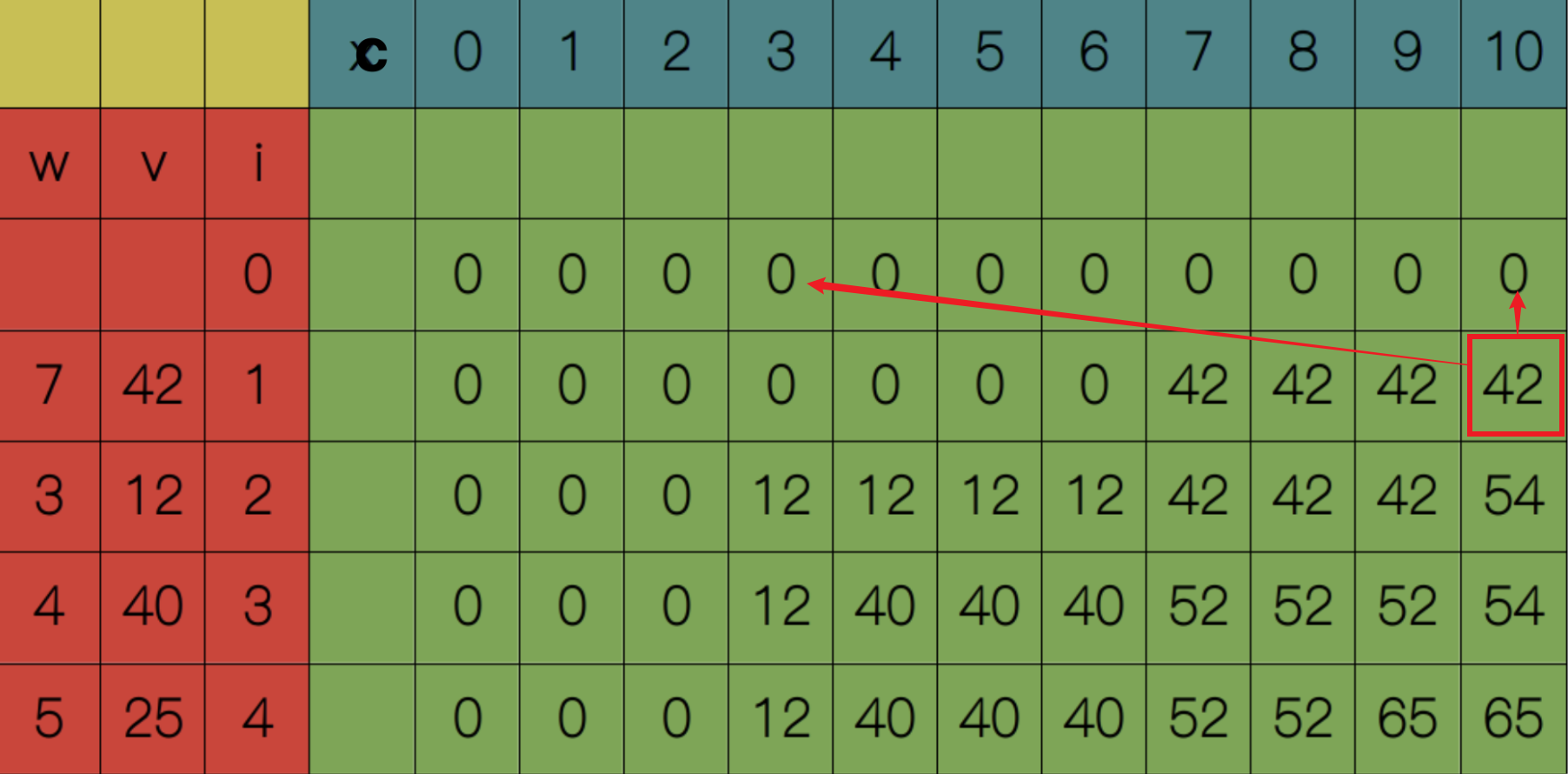
用一张 I * C 表格记录每个子问题的解,I表示物品数量,C表示背包容量。$S(0, c)$和$S(i, 0)$都等于0
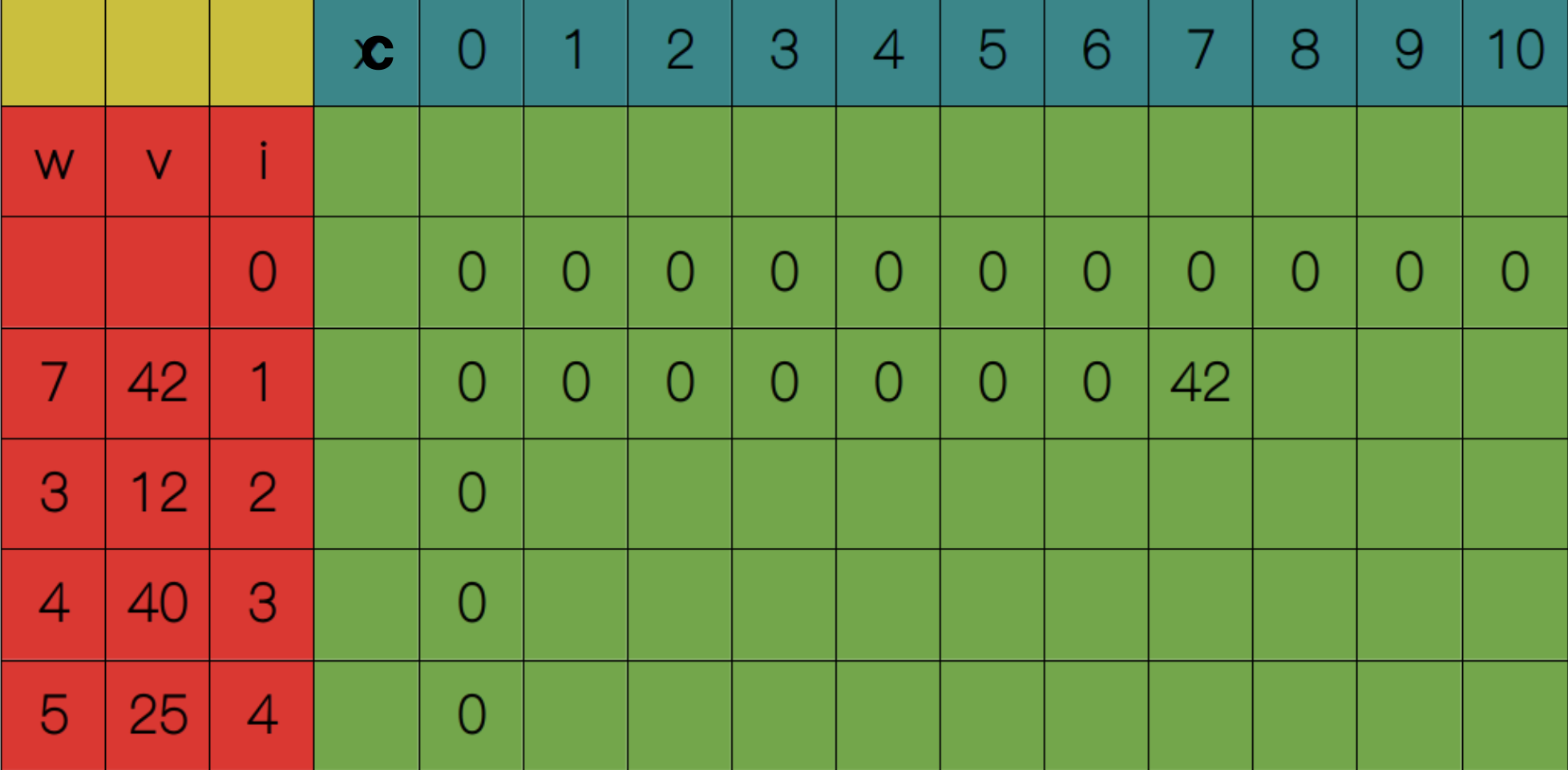
从$S(1, 1)$开始,显然$1 <= w_1$,所以$S(1, 1) = S(0, 1) = 0$。依次类推,直到$S(1, 7)$,此时$7 <= w_1$,所以$S(1, 7) = max(S(0, 7), S(0, 0) + 42) = 42$。
依次类推,直到填满整张表格,最终得到$S(4, 10) = 65$。
通过以上分析,可以得出自底向上的代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func knapsack_bottom_up(weights []int, values []int, capacity int) int {
table := make([][]int, len(weights)+1, len(weights)+1)
for j := 0; j < len(weights)+1; j++ {
row := make([]int, capacity+1, capacity+1)
table[j] = row
}
for i := 1; i < len(weights)+1; i++ {
for c := 1; c < capacity+1; c++ {
if weights[i-1] > c { // 不放入
table[i][c] = table[i-1][c] // 前一个物品在该容量下的最大价值
} else { // 放入
table[i][c] = int(
// table[i-1][c]是前一个物品在c容量下的最大价值,但不是一定包含 i-1 物品,需要 max 对比
math.Max(
// 前一个物品在该容量下的最大价值
float64(table[i-1][c]),
// 前一个物品在c-weights[i-1]容量下的最大价值 + 当前物品价值
// 因为 i 从 1 开始,所以要当前物品重量weights[i-1],价值同理
float64(table[i-1][c-weights[i-1]]+values[i-1]),
),
)
}
}
}
return table[len(weights)][capacity]
}
由于需要用到I * C的表格存储中间结果,空间复杂度和空间复杂度为O(IC)。
递归-自顶向下
着手解决原问题,先拆解成小问题,递归求解小问题,最终得到原问题的解。
对于第i个物品,要么放入,要么不放入。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func main() {
weights := []int{7, 3, 4, 5}
values := []int{42, 12, 40, 25}
capacity := 10
maxValue := knapsack_recursive(weights, values, len(weights), capacity)
fmt.Println(maxValue)
}
func knapsack_recursive(weights, values []int, i, c int) int {
// 递归出口
if i == 0 || c == 0 {
return 0
}
if weights[i-1] > c { // 超过过容量,不放入
return knapsack_recursive(weights, values, i-1, c)
} else { // 放入
return int(math.Max( // 考虑物品价值为负的场景
float64(knapsack_recursive(weights, values, i-1, c)),
float64(knapsack_recursive(weights, values, i-1, c-weights[i-1])+values[i-1]), // // 前一个物品在c-weights[i-1]容量下的最大价值 + 当前物品价值
))
}
}
时间复杂度$O(2^n)$:没个物品都有两种选择:放入和不放入,是一颗完全二叉树,深度为n,总共有$2^n$个节点
空间复杂度$O(n)$:递归调用栈为n
动态规划(备忘录)
和自低向上方式一样,先初始化一个I * C表格,每个单元格赋值-1 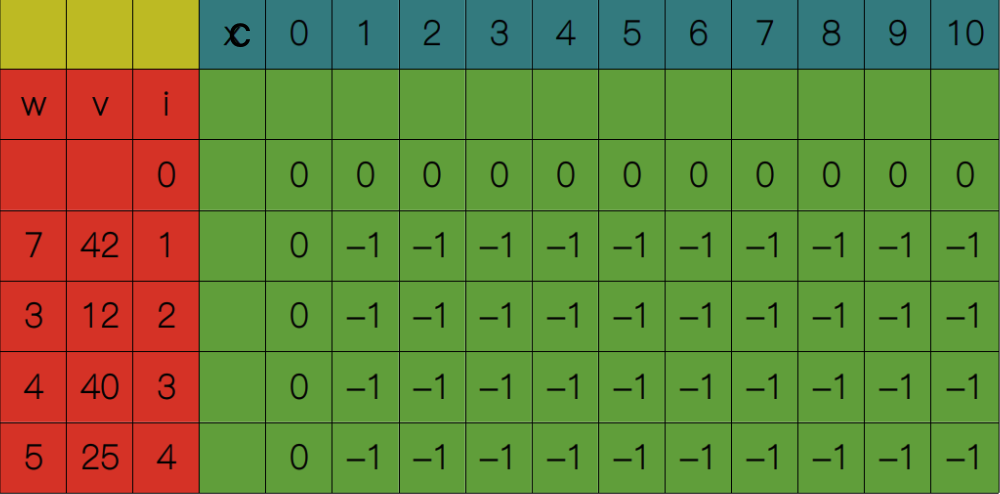
从$S(4,10)$开始,$S(4,10) = max(S(3,10), S(3, 5) + 25)$; $S(3,10) = max(S(2,10), S(2, 6) + 40)$, 以此递归,到递归出口$S(0,c) = 0$ 和 $S(i,0) = 0$。其中单元格不为-1,说明已经计算过,直接复用计算结果即可 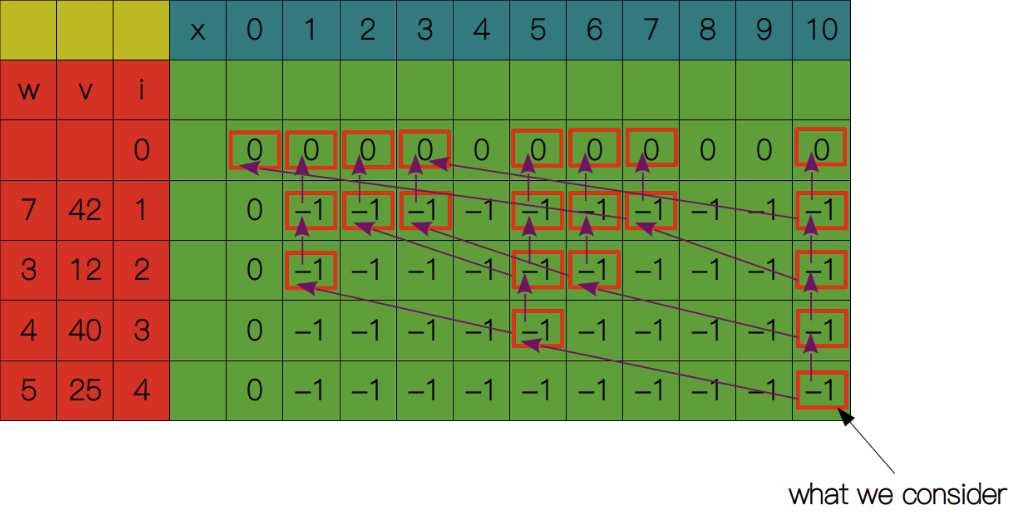
通过以上分析,自顶向下代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
func main() {
weights := []int{7, 3, 4, 5}
values := []int{42, 12, 40, 25}
capacity := 10
table := make([][]int, len(weights)+1, len(weights)+1)
table[0] = make([]int, capacity+1, capacity+1)
for j := 1; j < len(weights)+1; j++ {
row := make([]int, capacity+1, capacity+1)
for c := 1; c < capacity+1; c++ {
row[c] = -1
}
table[j] = row
}
maxValue := knapsack_top_down(table, weights, values, len(weights), capacity)
fmt.Println(maxValue)
}
func knapsack_top_down(table [][]int, weights, values []int, i, c int) int {
if table[i][c] < 0 {
if weights[i-1] > c { // 不放入
table[i][c] = knapsack_top_down(table, weights, values, i-1, c) // 前一个物品在c容量下的最大价值
} else {
table[i][c] = int(math.Max( // 考虑物品价值为负数场景
float64(knapsack_top_down(table, weights, values, i-1, c)),
float64(knapsack_top_down(table, weights, values, i-1, c-weights[i-1])+values[i-1]), // 前一个物品在c-weights[i-1]的最大价值 + 当前物品价值
))
}
}
return table[i][c]
}
时间复杂度O(I * C):因为使用备忘录,每个字问题最多被计算一次,最多有I * C个子问题
空间复杂度O(I * C):使用二维数组备忘录保存字问题处理结果,最多有I * C个子问题
优化空间-滚动数组
观察状态转移方程可知,计算$S(i, c)$时,只依赖于第 i-1 行正上方:$S(i-1, c)$和左上方:$S(i-1, c-w_i)$,所以只需要保存前一行数据即可。 而且计算当前行时,需要倒序遍历容量c,防止覆盖前一行数据。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func main() {
weights := []int{7, 3, 4, 5}
values := []int{42, 12, 40, 25}
capacity := 10
result := knapsackOptimizedSpace(weights, values, capacity)
println("Maximum value in Knapsack =", result)
}
// 从二维表计算流程理解:计算第 i 行,第 c 列的值时,只需要用到第 i-1 行正上方和左上方值
func knapsackOptimizedSpace(weights []int, values []int, capacity int) int {
dp := make([]int, capacity+1)
for i := 1; i < len(weights)+1; i++ {
for c := capacity; c > 0; c-- {
if c > weights[i-1] { // 数组不越界
dp[c] = int(math.Max(
float64(dp[c]), // 第 i-1 行,正上方
float64(dp[c-weights[i-1]]+values[i-1]), // 第 i-1 行,左上方;因为 i 从 1 开始,所以要减 1
))
}
}
}
return dp[capacity]
}
完全背包问题
题目描述
一共有N件物品,第i(i从1开始)件物品的体积为w[i],价值为v[i]。每个物品可以重复选取。在总体积不超过背包上限C的情况下,能够装入背包的最大价值是多少?
如:
1
2
3
4
5
6
物品1: weight=7, value=42
物品2: weight=3, value=12
物品3: weight=4, value=40
物品4: weight=5, value=25
背包容量C=10; 则最大价值为: 40 + 40 = 80
与0-1背包问题的区别在于,每个物品可以重复选取。
解题思路
与0-1背包问题类似,$S(i, c)$ 表示对与第 i 件物品,容量为 c 的背包,能获取的最大价值。则对于第 i 件物品,有放入和不放入两种选择:
1、不放入:与 0-1 背包问题相同,$S(i, c) = S(i-1, c)$
2、放入:由于物品可以重复选取,放入后,仍然可以选择放入该物品,$S(i, c) = S(i, c - w_i) + v_i$。同样需要和不放入情况对比,取最大值。则$S(i, c) = max(S(i-1, c), S(i, c - w_i) + v_i)$
为什么不需要考虑 i-1 物品在 c - w_i 容量场景:$S(i-1, c - w_i)$?
因为$S(i, c - w_i) + v_i$已经是 $S(i-1, c - w_i)$ 和 $S(i, c - w_i - x)$ 的最大值。
综上所述,状态转移方程如下:
与 0-1 背包问题只有一个区别:放入物品时,状态转移方程中,$S(i-1, c - w_i)$ 变为 $S(i, c - w_i)$。
动态规划-自底向上
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
func main() {
weights := []int{7, 3, 4, 5}
values := []int{42, 12, 40, 25}
capacity := 10
result := unboundedKnapsackDP(weights, values, capacity)
println("Maximum value in Knapsack =", result)
}
func unboundedKnapsackDP(weights []int, values []int, capacity int) int {
dp := make([][]int, 0, len(weights)+1)
for i := 0; i < len(weights)+1; i++ {
row := make([]int, capacity+1)
dp = append(dp, row)
}
for i := 1; i < len(weights)+1; i++ { // 遍历物品(列),从 1 开始
for c := 1; c < capacity+1; c++ { // 遍历容量(行),从 1 开始
if weights[i-1] > c { // 当前物品重量大于容量,不能放入背包
dp[i][c] = dp[i-1][c] // 等于上一个物品在 c 容量的价值
} else {
dp[i][c] = max( // 用 max 比较
dp[i-1][c], // 若单前物品价值为负数
// 因为物品可以多次放入,所以当前容量 c 下价值 = 当前物品在c-weights[i-1]时价值 + values[i-1]
// 因为 i 从 1 开始;当前物品索引为 i-1
dp[i][c-weights[i-1]]+values[i-1],
)
}
}
}
return dp[len(weights)][capacity]
}
优化空间-滚动数组
与 0-1 背包问题不同,计算$S(i, c)$时,依赖于当前行的左侧单元格$S(i, c-w_i)$,所以需要正序遍历容量c,防止覆盖当前行数据。 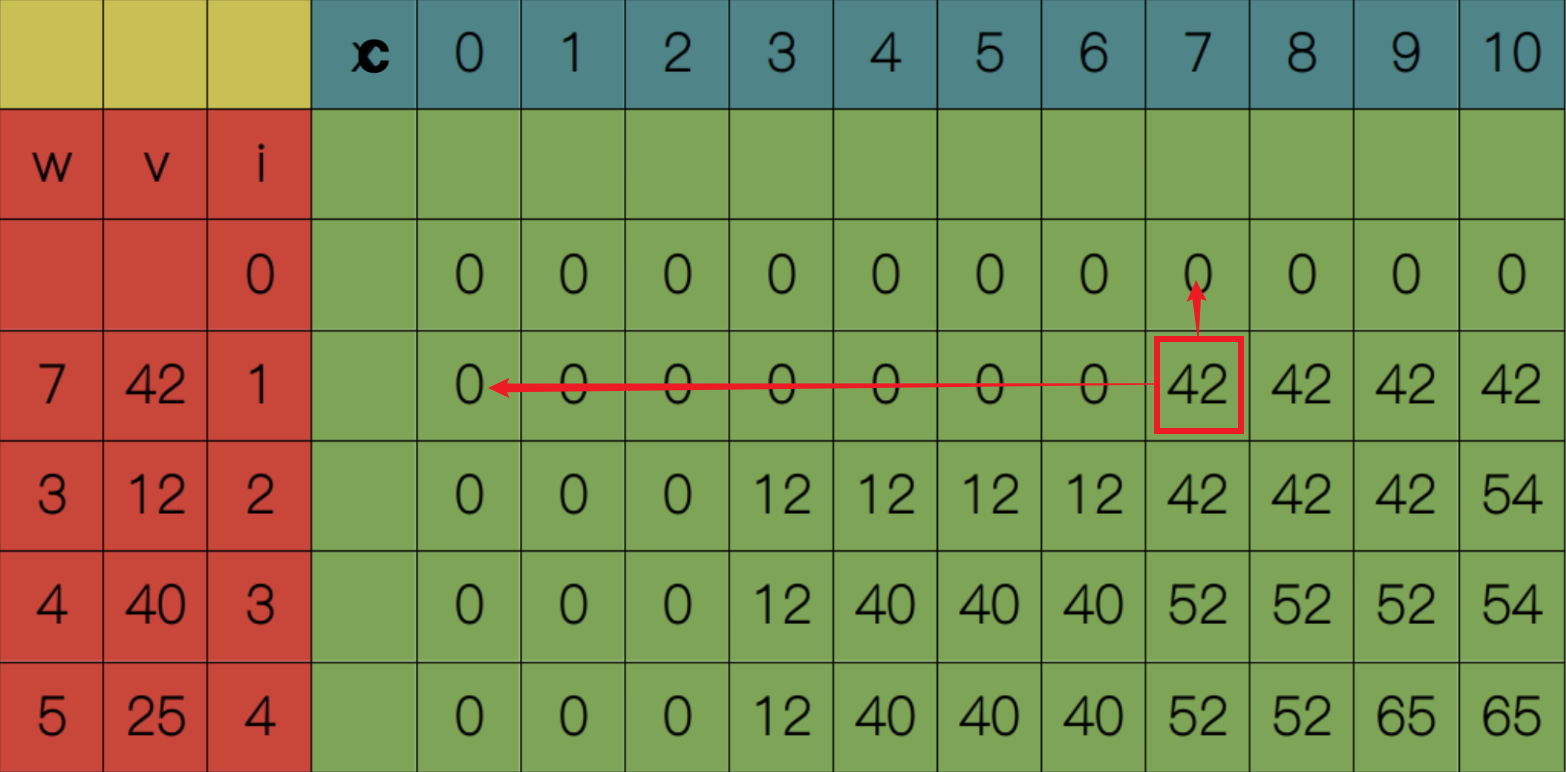
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func main() {
weights := []int{7, 3, 4, 5}
values := []int{42, 12, 40, 25}
capacity := 10
result := unboundedKnapsackDPComp(weights, values, capacity)
println("Maximum value in Knapsack =", result)
}
func unboundedKnapsackDPComp(weights []int, values []int, capacity int) int {
dp := make([]int, capacity+1)
for i := 1; i < len(weights)+1; i++ {
for c := 1; c < capacity+1; c++ { // 正序
if weights[i-1] > c { // 不放入
continue // 也就是:dp[c] = dp[c]
}
dp[c] = max(
dp[c], // 若物品价值为负数
// 因为物品可以多次放入,所以当前容量 c 下价值 = 当前物品在c-weights[i-1]时价值 + values[i-1]
// 因为 i 从 1 开始;当前物品索引为 i-1
dp[c-weights[i-1]]+values[i-1],
)
}
}
return dp[capacity]
}
Q&A
在构建动态规划表格时,为什么要从 1 开始?
在动态规划状态转移过程,table[i][c] = table[i-1][c],为了避免数组越界,i和c都需要从1开始。 当然也可以从 0 开始,只不过需要在代码中增加额外的判断逻辑,处理 i=0 或 c=0 的情况。
0-1 背包问题和完全背包问题的在实现上区别是什么?
动态规划转移方程不同
- 0-1 背包问题放入物品时,$S(i,c) = S(i-1, c-w_i) + v_i$
- 完全背包问题放入物品时,$S(i,c) = S(i, c-w_i) + v_i$。
优化空间方式实现遍历顺序不同
- 0-1 背包问题依赖正上方(不放入)和左上方(放入),所以需要倒序遍历容量 c,防止覆盖前一行数据。
- 完全背包问题依赖正上方(不放入)和左侧(放入),所以需要正序遍历容量 c,防止覆盖当前行数据。
参考
- 01背包问题:https://infinityglow.github.io/study/algorithm/dynamic-programming/knapsack-problem/
- 完全背包问题:https://www.hello-algo.com/chapter_dynamic_programming/unbounded_knapsack_problem/
分割等和子集-416
题目描述
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 100
解题思路
求分割成两个相等的子集,也就是找到是否存在一个子集等于sum / 2。
可以转化成背包问题,背包容量是 sum / 2,物品重量和价值都是 nums。从 nums 中寻找 n 个物品放入背包,重量刚好是 sum / 2。 对于这道题,我们只需要关注重量,即 nums 是物品重量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
func canPartition(nums []int) bool {
if len(nums) < 2 {
return false
}
sum := 0
for _, num := range nums {
sum += num
}
if sum%2 != 0 {
return false
}
// target(容量),获取能容纳子集数组最大值
target := sum / 2
// dp[i][t]标志在 t 容量时,子集数组最大值
dp := make([][]int, len(nums)+1)
// 第 i 行依赖第 i-1 行结果,为方便取值,初始化第一个行(i=0)为零值
dp[0] = make([]int, target+1)
// 外层遍历物品
for i := 1; i < len(nums)+1; i++ {
// 待填充行
row := make([]int, target+1)
// 内层遍历容量
// t从 1 开始是为了方便下标计算,也可以从 0 开始
for t := 1; t < target+1; t++ {
if t-nums[i-1] >= 0 {
// 放的下
// 注意做 max 对比
row[t] = max(
dp[i-1][t],
// 前一个 num,在 t-nums[i-1](容量),再加上当前 num 值
dp[i-1][t-nums[i-1]]+nums[i-1],
)
} else {
// 容量不足,放不下,等于上一个num(物品)在 t(容量)下的值
row[t] = dp[i-1][t]
}
}
dp[i] = row
}
// 一顿操作下来,如果最大的子集只和刚好等于 target,则存在这样的子集
return dp[len(nums)][target] == target
}
总结:
- 关注价格,背包问题可以求最大价值
- 关注重量(容量),背包问题可以求是否装满
最后一块石头的重量II-1049
题目描述
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎; 如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。 最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40]
输出:5
提示:
1 <= stones.length <= 30
1 <= stones[i] <= 100
解题思路
题意可以转化成把石头堆分成两份,而且每堆重量尽可能相同,也就是接近 sum / 2。
这里就非常像【分割等和子集-416】问题,只不过【分割等和子集-416】问题是求背包是否正好装满,该题是求 sum / 2 容量下最大能装多少。
用一维dp数组记录状态,dp[j]表示j容量下,最多能装的石头重量。第一堆最大能装重量:dp[sum / 2],另一堆最大能装重量是:sum - dp[sum / 2];则一起粉碎后后剩余:(sum - dp[sum / 2]) - dp[sum / 2]
为什么分堆容量限制是 sum/2,而不用考虑 sum 是奇数的情况?
因为sum是奇数场景下,两堆重量不可能相等。sum/2向下取整,第一堆分到dp[sum / 2],第二堆分到sum - dp[sum / 2]。也可以限制sum/2+1,只不过一、二重量对换。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func lastStoneWeightII(stones []int) int {
if len(stones) == 1 {
return stones[0]
}
sum := 0
for i := 0; i < len(stones); i++ {
sum += stones[i]
}
target := sum / 2
dp := make([]int, target+1)
for i := 0; i < len(stones); i++ {
for j := target; j > 0; j-- {
if j-stones[i] >= 0 {
dp[j] = max(dp[j], dp[j-stones[i]]+stones[i])
}
}
}
return sum - dp[target] - dp[target]
}
目标和-494
题目描述
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-‘ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-‘ ,然后串联起来得到表达式 “+2-1” 。 返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
提示:
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
解题思路
所有添加 ‘+’ 的数字归为 left,所有添加 ‘-‘ 的数字归为 right,则有:left - right = target 。 所有数字之后为 sum ,$left - right = target$ -> $left - (sum-left) = target$ -> $left = (sum + target)/2$。 最终转化成求nums有多少种和为 left 的子集。
为什么不是求和为 right 的子集?
求 left 或 right 子集结果一致
(sum + target)/2 有余数怎么办?凉拌,那么就是不存在这样组合,直接返回 0
dp[i][j]表示前 i 个数,满足元素和为 j 的组合数。有两种情况;
1、第 i 个元素不放入组合;nums[i] > j;则 dp[i][j] = dp[i-1][j]
2、第 i 个元素放入组合;则 dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]]
1
不懂
一和零-474
题目描述
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1
输出:2
解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 '0' 和 '1' 组成
1 <= m, n <= 100
零钱兑换 II-518
题目描述
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
示例 1:
输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入:amount = 3, coins = [2]
输出:0
解释:只用面额 2 的硬币不能凑成总金额 3 。
示例 3:
输入:amount = 10, coins = [10]
输出:1
提示:
1 <= coins.length <= 300
1 <= coins[i] <= 5000
coins 中的所有值 互不相同
0 <= amount <= 5000
解题思路
根据题意,求凑成总金额硬币组合数,而且每种面额硬币有无限个,属于完全背包问题。
设 dp[i][j] 表示前 i 种硬币,凑成金额 j 的组合数。则有两种情况:
1、不选取第 i 种硬币; 硬币面额 > j
\[dp[i][j] = dp[i-1][j]\]2、选取第 i 种硬币; 则等于不选取第 i 种硬币的组合数 + 选取第 i 种硬币后的组合数
\[dp[i][j] = dp[i-1][j] + dp[i][j - coins[i]]\]为什么不用考虑 dp[i-1][j - coins[i]]?
因为dp[i][j - coins[i]]已经是 dp[i-1][j - coins[i]] 和 dp[i][j - coins[i] - x] 之和
临界条件:当正好选了coins[i],就可以凑成金额j,也就是 j == coins[i], 有 1 种方式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
func change(amount int, coins []int) int {
dp := make([][]int, len(coins)+1)
for i := range dp {
dp[i] = make([]int, amount+1)
// 临界条件: 当正好选了coins[i],就可以凑成金额j,也就是 j == coins[i], 有 1 种方式
dp[i][0] = 1
}
for i := 1; i < len(coins)+1; i++ {
for j := 0; j < amount+1; j++ {
if j < coins[i-1] { // 当前硬币面值大于金额,不能选取
dp[i][j] = dp[i-1][j]
} else {
dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]]
}
}
}
return dp[len(coins)][amount]
}