背包问题
0-1背包问题
题目描述
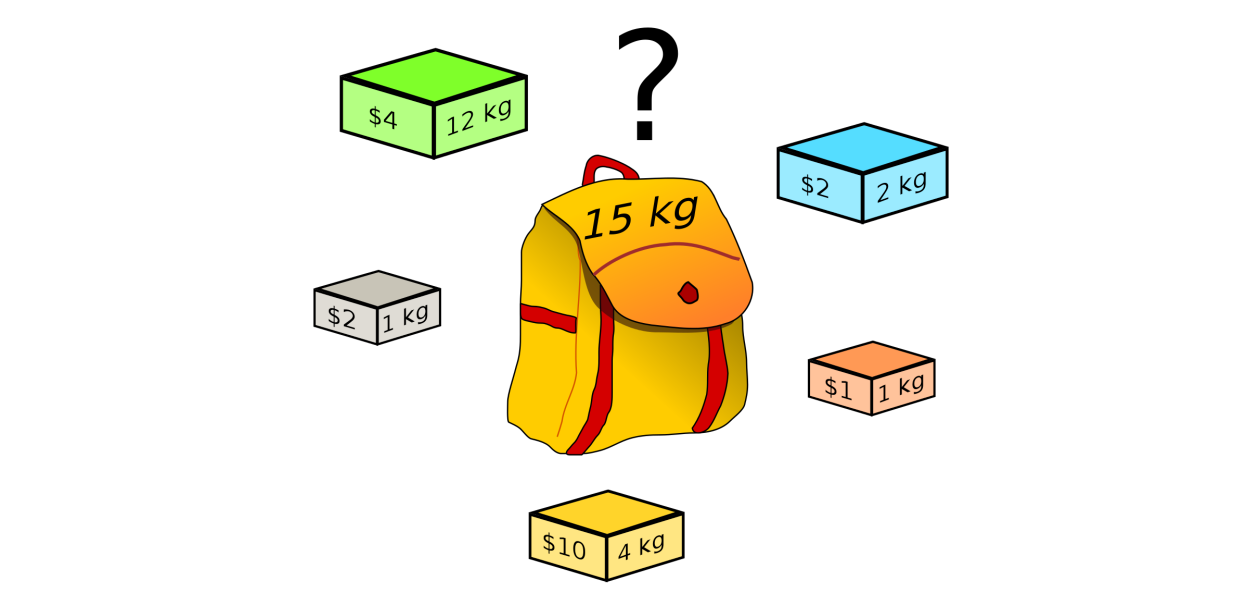
一共有N件物品,第i(i从1开始)件物品的体积为w[i],价值为v[i]。在总体积不超过背包上限C的情况下,能够装入背包的最大价值是多少?
如:
1
2
3
4
5
6
物品1: weight=7, value=42
物品2: weight=3, value=12
物品3: weight=4, value=40
物品4: weight=5, value=25
背包容量C=10; 则最大价值为: 40 + 25 = 65
解题思路
$S(i, c)$ 表示对与第 i 件物品,容量为 c 的背包,能获取的最大价值。则对于第 i 件物品,有放入和不放入两种选择:
1、选择不放入: 第 i 件物品重量超过背包容量,$w_i > c$。则只能选择不放入,$S(i, c) = S(i-1, c)$。
2、选择放入: 第 i 件物品重量不超过背包容量,$w_i \le c$。则可以选择放入,$S(i, c) = S(i-1, c - w_i) + v_i$。 $v_i$可能是负数,所以需要和不放入情况对比,取最大值。则$S(i, c) = max(S(i-1, c), s(i, c - w_i) + v_i)$
3、临界条件: 当没有物品或者背包容量为0时,最大价值为0,即$S(0, c) = 0$或$S(i, 0) = 0$。
综上所述,状态转移方程如下:
自底向上
从解决子问题出发,逐步解决大问题。
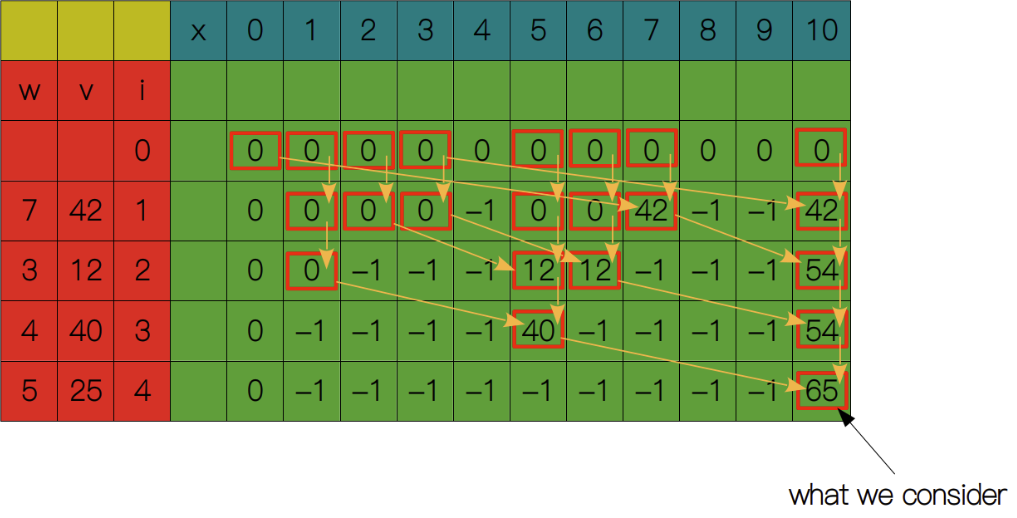
用一张 I * C 表格记录每个子问题的解,I表示物品数量,C表示背包容量。$S(0, c)$和$S(i, 0)$都等于0
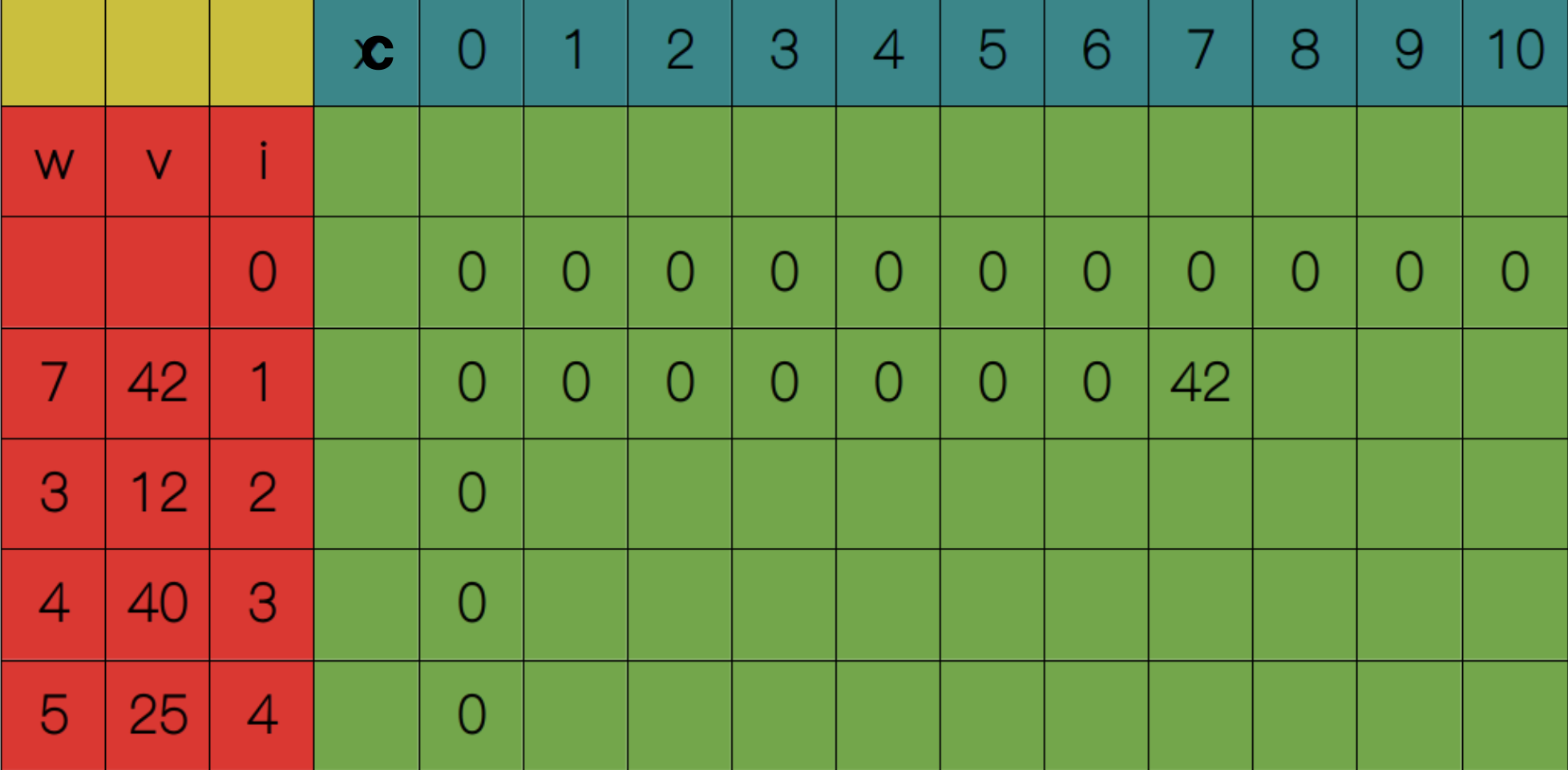
从$S(1, 1)$开始,显然$1 <= w_1$,所以$S(1, 1) = S(0, 1) = 0$。依次类推,直到$S(1, 7)$,此时$7 <= w_1$,所以$S(1, 7) = max(S(0, 7), S(0, 0) + 42) = 42$。
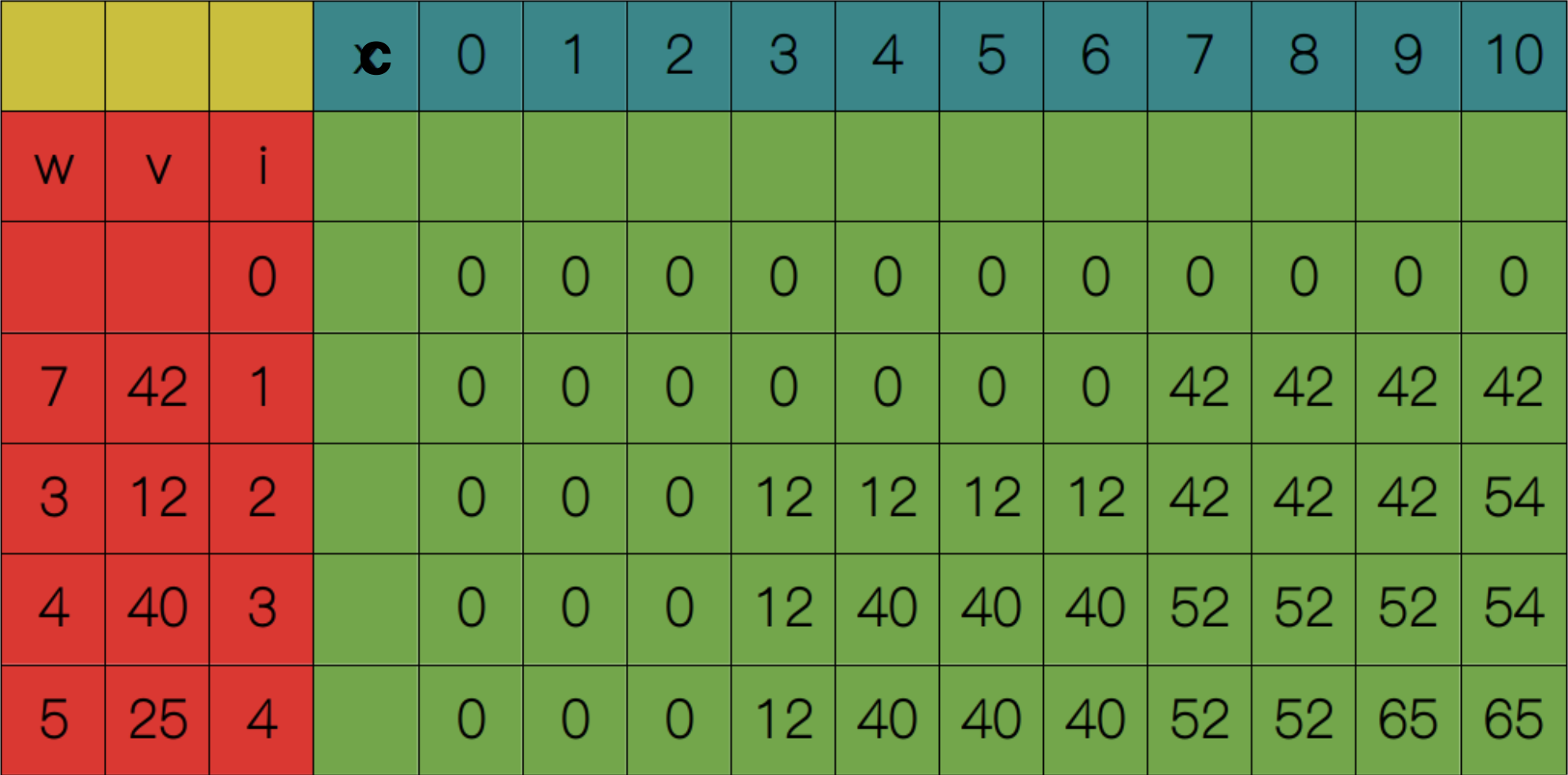
依次类推,直到填满整张表格,最终得到$S(4, 10) = 65$。
通过以上分析,可以得出自底向上的代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func knapsack_bottom_up(weights []int, values []int, capacity int) int {
table := make([][]int, len(weights)+1, len(weights)+1)
for j := 0; j < len(weights)+1; j++ {
row := make([]int, capacity+1, capacity+1)
table[j] = row
}
for i := 1; i < len(weights)+1; i++ {
for c := 1; c < capacity+1; c++ {
if weights[i-1] > c { // 不放入
table[i][c] = table[i-1][c] // 前一个物品在该容量下的最大价值
} else { // 放入
table[i][c] = int(
math.Max( // 考虑物品价值为负数情况,取最大值
float64(table[i-1][c]), // 前一个物品在该容量下的最大价值
float64(table[i-1][c-weights[i-1]]+values[i-1]), // 前一个物品在c-weights[i-1]容量下的最大价值 + 当前物品价值
),
)
}
}
}
return table[len(weights)][capacity]
}
由于需要用到I * C的表格存储中间结果,空间复杂度和空间复杂度为O(IC)。
自顶向下
着手解决原问题,先拆解成小问题,递归求解小问题,最终得到原问题的解。
递归
对于第i个物品,要么放入,要么不放入。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func main() {
weights := []int{7, 3, 4, 5}
values := []int{42, 12, 40, 25}
capacity := 10
maxValue := knapsack_recursive(weights, values, len(weights), capacity)
fmt.Println(maxValue)
}
func knapsack_recursive(weights, values []int, i, c int) int {
// 递归出口
if i == 0 || c == 0 {
return 0
}
if weights[i-1] > c { // 超过过容量,不放入
return knapsack_recursive(weights, values, i-1, c)
} else { // 放入
return int(math.Max( // 考虑物品价值为负的场景
float64(knapsack_recursive(weights, values, i-1, c)),
float64(knapsack_recursive(weights, values, i-1, c-weights[i-1])+values[i-1]), // // 前一个物品在c-weights[i-1]容量下的最大价值 + 当前物品价值
))
}
}
时间复杂度$O(2^n)$:没个物品都有两种选择:放入和不放入,是一颗完全二叉树,深度为n,总共有$2^n$个节点
空间复杂度$O(n)$:递归调用栈为n
动态规划(备忘录)
和自低向上方式一样,先初始化一个I * C表格,每个单元格赋值-1 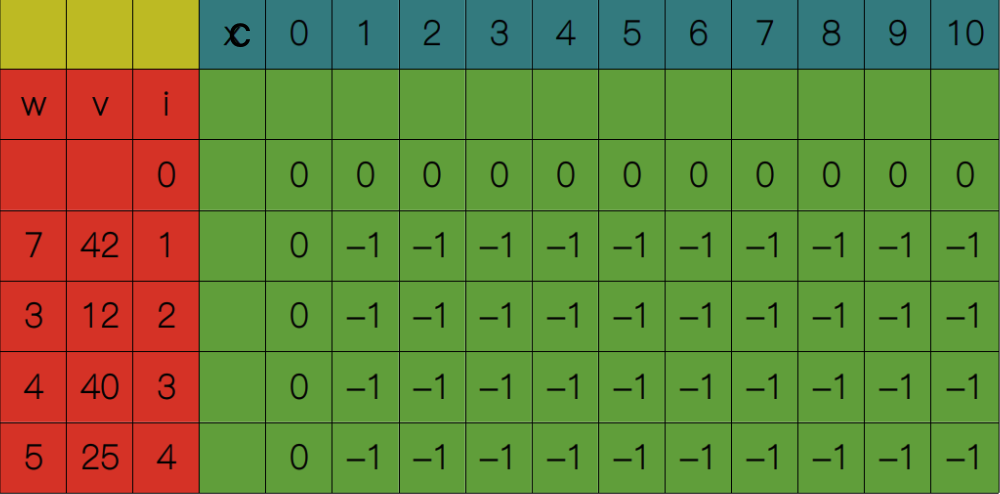
从$S(4,10)$开始,$S(4,10) = max(S(3,10), S(3, 5) + 25)$; $S(3,10) = max(S(2,10), S(2, 6) + 40)$, 以此递归,到递归出口$S(0,c) = 0$ 和 $S(i,0) = 0$。其中单元格不为-1,说明已经计算过,直接复用计算结果即可 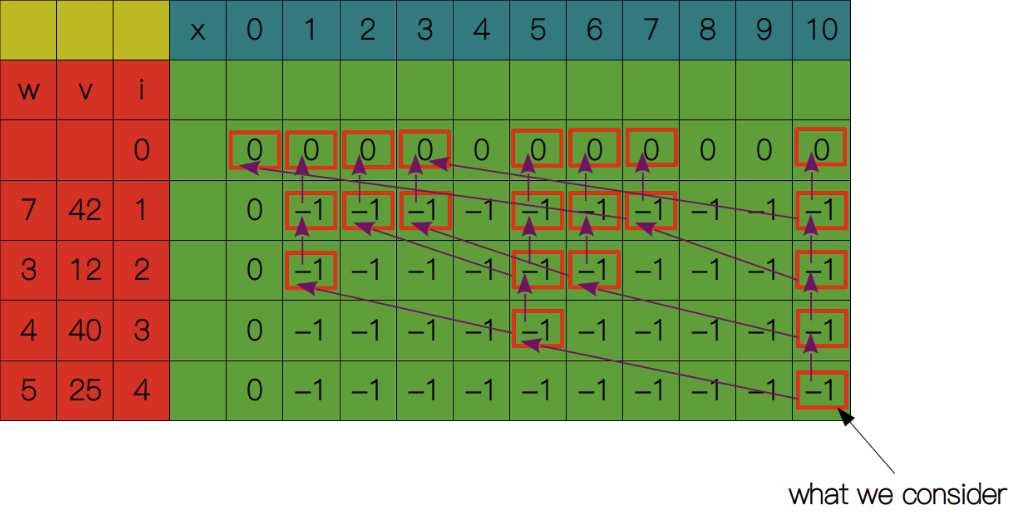
通过以上分析,自顶向下代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
func main() {
weights := []int{7, 3, 4, 5}
values := []int{42, 12, 40, 25}
capacity := 10
table := make([][]int, len(weights)+1, len(weights)+1)
table[0] = make([]int, capacity+1, capacity+1)
for j := 1; j < len(weights)+1; j++ {
row := make([]int, capacity+1, capacity+1)
for c := 1; c < capacity+1; c++ {
row[c] = -1
}
table[j] = row
}
maxValue := knapsack_top_down(table, weights, values, len(weights), capacity)
fmt.Println(maxValue)
}
func knapsack_top_down(table [][]int, weights, values []int, i, c int) int {
if table[i][c] < 0 {
if weights[i-1] > c { // 不放入
table[i][c] = knapsack_top_down(table, weights, values, i-1, c) // 前一个物品在c容量下的最大价值
} else {
table[i][c] = int(math.Max( // 考虑物品价值为负数场景
float64(knapsack_top_down(table, weights, values, i-1, c)),
float64(knapsack_top_down(table, weights, values, i-1, c-weights[i-1])+values[i-1]), // 前一个物品在c-weights[i-1]的最大价值 + 当前物品价值
))
}
}
return table[i][c]
}
时间复杂度O(I * C):因为使用备忘录,每个字问题最多被计算一次,最多有I * C个子问题
空间复杂度O(I * C):使用二维数组备忘录保存字问题处理结果,最多有I * C个子问题
完全背包问题
参考
- 01背包问题:https://infinityglow.github.io/study/algorithm/dynamic-programming/knapsack-problem/
- 完全背包问题: