树与表

节点的度

• 节点有几个分叉

高度

• 自底向上，叶子节点的高度为1
• 树高logN

深度

• 自顶向下，根节点的深度为1

二叉树

• 定义：
  • 任意节点的度不超过2
• 查找时间复杂度：logN，递归深度logN；最坏情况下N
• 查找空间复杂度：logN，递归使用的栈空间；最坏情况下是N
• 遍历时间复杂度：N，每个节点都遍历
• 遍历空间复杂度：N，递归使用的栈空间

完全二叉树

• 叶子结点只能出现在最下层和次下层
• 最下层的叶子结点集中在树的左部

  满二叉树

• 任意一个节点都有两个孩子

二叉查找树

• 左子树小于根节点
• 右子树大于根节点
• 时间复杂度：O(logN)，最坏时间复杂度O(N)
• 空间复杂度为 O(logN)，，最坏时间复杂度O(N)

AVL树（平衡二叉树）

• 定义：
  • 满足二叉查找树的基础上
  • 任意节点左右子树高度差（平衡因子）<=1
• 优点：
  • 查询效率稳定
• 缺点：
  • 维护平衡成本高
• 应用场景：
  • 插入少，查询多的场景
• 时间复杂度：递归数的高度，O(logN)，不会出现最差情况
• 空间复杂度：为 O(logN)，不会出现最差情况

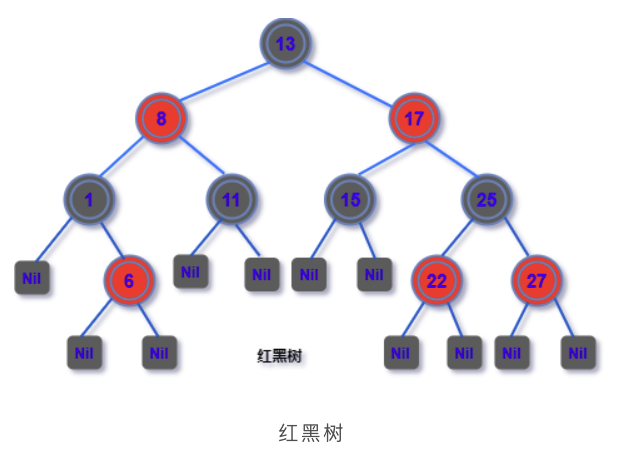
红黑树

• 任意节点的左右子树的高度，相差不超过2 倍。
• 树根是黑色
• 叶子节点是黑色
• 时间复杂度：O(logN)

• 空间复杂度为 O(logN)

  

  • 保证较高的插入和删除效率
  • 优点：
    • 不追求完全平衡，减少自旋
    • 兼顾删除和插入的效率
  • 缺点：
    • 查询效率比平衡二叉树略低
  • 应用场景：
    • 操作系统虚拟内存管理、hashmap键存储
    • epoll管理事件

B树

• 任意节点左右子树高度差（平衡因子） == 0
• 节点可以保存多个数据

• 时间复杂度：O(logN)

  

B+树

• 非叶子节点只保存索引，不保存数据
• 叶子节点保存数据，并形成链表结构
• 时间复杂度：O(logN)

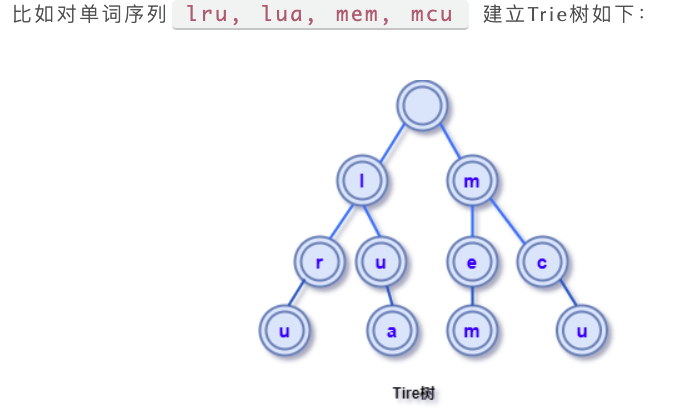
Trie树（前缀树或字典树）

• 根节点不包含字符，非根节点只包含一个字符

• 从根节点到某个节点，途经字符连起来就是该节点对应的字符串

  

  • 应用：
    • 搜索引擎提示词
    • https://cloud.tencent.com/developer/article/1556054

跳表

https://juejin.cn/post/6844903955831619597

• 优点：
  • 更新时，局部性更好
  • 支持范围查询
• 缺点：
  • 占空间
• 应用场景：
  • 内存多级页表
  • redis key管理
  • redis zset类型
• 时间复杂度：近似二分查找，等于 索引高度：logn * 每层索引遍历元素的个数 = logn
• 空间复杂度：n/2（一级索引） + n/4（二级索引） + n/8（三级索引） + … + 8 + 4 + 2 = n-2，空间复杂度是 O(n)

    redis中为啥用跳表而不用红黑树
    1、更新时，跳表需要更新的范围更小，竞争锁的开销更小，并发高
    https://blog.csdn.net/qq9808/article/details/104865385
  

哈希表

• 优点：
  • 时间复杂度O(1)
• 缺点：
  • 基于数组，扩充成本高，大数据量性能下降严重
  • 存在hash冲突
  • 不支持范围查询
• 应用场景：
  • map结构

区别（维度）

• 时间复杂度，空间复杂度
• 是否有序
• 可扩展性

参考：

• https://jishuin.proginn.com/p/763bfbd2febb